同济大学土木工程防灾减灾全国重点实验室庄晓莹教授关于 Multi-connected boundary conditions in solid mechanics and surgery theory 的论文发展了原创性工作，经评委会评议决定授予计算力学 2023 年巴特研究奖 (Bathe Award 2023)。

    K. J. Bathe Award是计算力学工程领域最佳青年研究者论文奖，该奖项以麻省理工学院机械工程教授 Klaus-Jürgen Bathe 命名。Bathe 教授是国际计算力学领域的先驱之一，也是著名的非线性多场耦合 ADINA 软件的创始人。

    庄晓莹教授主要研究领域为土木工程先进材料与多尺度力学。她开发了许多创新和稳健的数值方法，包括水平集方法、单位分解法 (如无网格法、XFEM、虚拟节点法和有限覆盖法)、多尺度方法、相场模型和误差驱动的自适应方法。她将创新的数值方法应用于土木工程、固体物理与材料科学中的复杂问题。将上述放法用于求解处理耦合 (流固、热力、热流固和电力) 问题、不确定性分析/不确定性量化以及反问题和优化过程等。先后获得由洪堡基金会资助的 Sofja Kovalevskaja 奖 (2015，165万欧元)，莱布尼茨青年科学家奖 (2018)，德国科学名人堂青年科学探索奖 (2019)，Engineering Geology 国际期刊年度最佳论文奖 (2021)，中国岩石力学与工程学会自然科学特等奖等国内外重要奖项 (2021)。

摘  要

    边界条件对偏微分方程（PDEs）至关重要，因为它们约束PDEs并确保解的存在性和唯一性。基于流形的组合和拓扑手术理论，我们提出了多元素边界条件，作为经典力学中传统边界条件（包括Dirichlet条件、Neumann边界条件和Robin边界条件）的推广。多元素边界/域条件将不同边界或域上的物理量粘合在一起，其实现过程通过局部坐标系上建立了几个边界上的点对点对应（点映射），并通过“虫洞”（即约束方程）实现了不同域上的相互作用。对弱形式的研究表明，一般的多元素边界条件与变分原理/加权残差方法不一致。为了避免这种困境，我们提出了一种基于增广拉格朗日方法和非局部算子方法（NOM）的数值方案，用于处理具有一般多元素边界条件的力学问题。数值试验表明，不同的多元素边界条件下，结构具有完全不同的变形模式。

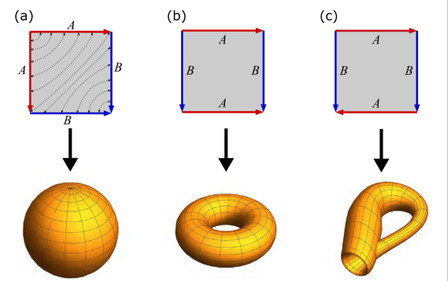
图1：拓扑手术通过将具有相同符号和方向的两边粘合在一起来形成不同的形状。例如，在（a）中，将虚线穿过的点粘合在一起形成球面。

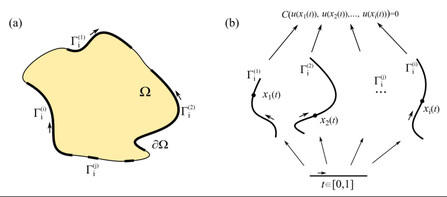
图2：二维i元边界条件的示意图 (a)选择i个边界形成i-元素边界； (b)基于局部坐标系t ∈[0, 1]的坐标元组（x₁(t),x₂(t),⋯,xᵢ(t)）,并建立物理量之间的相互作用方程。

参考:

https://www.sciencedirect.com/journal/computers-and-structures/about/news#the-k-j-bathe-award-2023

https://www.bhvt.uk/batheaward2018/

原文链接：

https://www.sciencedirect.com/science/article/pii/S0045794921000262?via%3Dihub